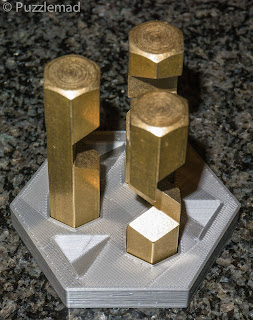Yet again, I am so so grateful to my wonderful foreign correspondent Mike
Desilets for coming to my rescue and producing an absolutely fabulous blog
post for us all. I seem to have failed to solve anything this last week or so
and have been concentrating on compiling my annual top 10(ish) for the year.
Just when I need it most Mike springs into action - I don't even have to ask
him as he just seems to know when I need his help. Over to you mate...
Aloha kākou puzzlers,
This week’s PuzzleMad Sunday Edition (the thick one with all the adverts) (Ed - thick one? You sound like Mrs S!) comes to you from the Hawaii Foreign Office, by way of Florida, where I sit
in a motel room awaiting COVID test results prior to a visit with my
pre-existing parents (Ed - why are your parents pre-existing?).
Infection is only a remote possibility, but I spare no inconvenience for
family. The whole situation has left me with nothing but time, and how better
to use perfectly good time than by talking about great puzzles.
This week I am thrilled to present a recent and quite-hard-to-get-hold-of
puzzle by designer Christian Cormier - Plant Cycle. This post has actually
been overtaken by events, as Christian has just released his latest puzzle,
Billiards. But we will ignore that inconvenient truth for the nonce.
This is not the first coverage of Plant Cycle.
Fivesinatras
has already provided the community with a great (and timelier) review which
you can find over here. Fivesinatras is spot on and I basically agree with
everything he has to say on the matter. But of course, you can’t get too many
takes on cool mechanical puzzles, and Christian’s Plant Cycle is both cool and
mechanical.

|
|
Plant Cycle is one hefty puzzle.
|
Plant Cycle is one of a growing number of truly
MASSIVE puzzles, joining
the ranks of the recent Popplocks and the unrelenting stream of toe-breaking,
floor-denting puzzles from the pan-hexual duo at
TwoBrassMonkeys. I couldn’t be happier with this trend, other than the fact that it has made
me poorer of purse (
Ed - me too!). This class of puzzle will do great
damage to your account over a very short span of time. They may even force you
to make hard choices, especially if you also collect box and burr (
Ed - yes, I may have to trade Mrs S in for a line of credit on
puzzles...Whack! Ouch!). This is not necessarily a bad thing, though, as any veteran collector (of
anything) will tell you. Completionism is a harsh mistress, serving a
frustratingly elusive form of satisfaction. It’s just my opinion of course, but
I believe the average puzzle bloke should thoughtfully channel this urge. After
all, it is the overall quality of your puzzle collection, by your own
self-concocted standard, that is important. Budgetary limits force one to think
deliberately about motivations, objectives, and which puzzles are likely to
bring the most long-term pleasure. Fiscal realities can be an incentive to focus
yourself and increase your puzzling happiness. With focus, the stress associated
with “missing out” on so many cool puzzles is greatly reduced (but not gone).
This advice goes well beyond puzzles, of course. Alternatively, you can just get
a second or third job, like my nocturnal friend Kevin. But then when are you
going to solve? It’s a true conundrum, like my nocturnal friend Kevin (
Ed - do you mean me? If only I was nocturnal...then I could have time to
solve some puzzles. Unfortunately I am just insomniac but not usefully so).

|
| Keys down. |
But let’s say, optimistically, that you do have money to burn, and
furthermore that you love massive metal door-stopper puzzles that are fun,
interesting, and unique. Well in that case, good reader, you should have
purchased one of the 50 Plant Cycles manufactured by Christian a few years
back. Being somewhat of a puzzle hermit, and not knowing a Cormier from a
Cormorant, I completely missed it myself. My abiding disdain for
Facebook
did
NOT help. As it happens, a huge portion of the puzzle community
is active on Facebook. Dr Kevin Sadler, my oldest and best friend, boon
companion, Tom Sawyer to my Huck Finn (
Ed - are you after something?), has kept this information from me and will never be forgiven (
Ed - but haven't you read this blog for the last few years? I constantly
mention the FB community!).

|
|
Seed and sprout
|
Happily, a copy eventually crossed my path. I bought it without any
foreknowledge, or forethought for that matter. It really is a beast,
weighing in at just under a case of Spam (a traditional Hawaiian unit of
measure) (
Ed - a whole case? Or a can?). As you can see, it has a
nicely rounded triangular outline, no sharp edges, and is quite comfortable
to hold. The steel plate construction is the first thing you notice; a
technique not often seen. This gives a nice texture to the exterior and
provides visual interest. Upon closer inspection, you notice some
gear-looking components on each of the three corners; obviously something to
pay attention to. There is also a teeny tiny hole on each side. The
instructions don’t indicate what this is, but I’ll tell you anyway: it’s an
access hole for the rest tool. It’s not part of the solving process. The
bottom is featureless, brushed stainless. The top is where the real action
is. Plant Cycle sports three keys, each embedded into the guts of the puzzle
in its own private keyhole. The top of each key has a plant-related cut-out.
Per the theme of the puzzle, the cut-outs represent three stylized stages of
a flowering plant’s life cycle: seed, seedling, and flower. Nicely done. The
keys are clearly hand fabricated, which adds very much to their charm.
I interrupt myself here to point out that Plant Cycle does have an
antecedent - Father and Son Dueling Keys. I don’t have that puzzle, and
likely never will. As I understand it, Plant Cycle builds on that smaller
two-key puzzle, so perhaps I don’t really need it after all. That said, if
anyone has one, I am in the market!

|
|
Father and Son Dueling Keys.
|
The goal of Plant Cycle, if you have not already guessed, is to remove all
of the keys from the stainless body. They all have lots of play, and will
turn this way and that, and also will shift up and down, with some
manipulation. It isn’t at all clear what is holding the keys in, but with
proper turning and navigation, they will all rise up tantalizingly, and
one looks like it should pop out at any second. Alas, they are not going
to come out by random fiddling. In fact, I can tell you for certain, you
will never get any individual key out by simple jiggering. You will have
to start thinking about what you are looking at, and also perhaps about
the theme of the puzzle. “Plant Cycle” is a useful clue, and not just a
pretty name.

|
|
As far as they go with normal manipulation.
|

|
| Almost there! |
With some further key-wise exploration, you should make a certain discovery
about the internals. If exploited properly, that will get you pretty far.
This is actually quite a huge step. Once you figure this out, and make some
connections, you should be able to release your first key. What a great
feeling! Making progress is a huge relief. At this point, one key out, I
started to feel that Plant Cycle was going to be a great puzzle. There was
something very systematic going on inside, and I felt that despite working
“blind”, I could make some logical deductions based on feedback from the
internals. It was also clear at this point that getting the other keys out
was not going to be as simple as doing the same thing for each key. All the
parts were related somehow. One might even say there was a “cycle”
involved.
Once you get the keys out, they can be reinserted by largely the reverse
process. This should not be too tough since, by now, you understand the
internals much better. Still, since you are working blind, it will take a
little work and is definitely non-trivial. If you somehow manage, beyond all
odds, to release all three keys without understanding what you were doing,
then it will probably take you quite some time to return them, if ever you do.
A little tool is provided to expedite the reset process. This makes it a
little faster, but as mentioned on the instructions, it’s not
required.

|
|
Instructions and reset tool.
|
Honestly, that’s about all I can tell you, and even that might be too much for
some. I can add this: I would classify Plant Cycle loosely as sequential
discovery. No, a hex wrench won’t pop out of a hidden compartment, but the
solving process is very much sequential, and the keys can be thought of as
tools that you need to learn how to use to make progress. There are distinct
stages of discovery and learning with this puzzle which make it very
enjoyable. It is also an interesting twist on the puzzle lock; an inverse
lock, if you will. There is no hasp and the keys themselves are “locked”
within the body. Possibly not a conceptual first (consult your local
metagrobologist), but I would wager it’s a very strong contender for most
advanced application. And most massive. (Ed - How does it compare in mass to one of the last 2 Popplocks - The T11
was ginormous!)

|
|
Kevin, this little detail looks important.
|
Overall, I enjoyed Plant Cycle very much. This is not an insanely tough
puzzle, and I don’t think that was Christian’s goal in creating it. It is
instead a reasonably difficult puzzle with a solution that requires
exploration, discovery, thought, and ultimately an understanding of the
internal mechanics. Also, and of supreme importance to me personally, it is
something new. Plant Cycle gave me a new and different solving experience,
which is really what this whole thing is all about. For that I thank
Christian. I am also more excited than ever to try out Billiards, which
looks to be a completely different puzzle. Perfect!
Now for the fun part. As Kevin and I try tell you, time after time,
PuzzleMad is a Full Service Blog (Ed - actually Mike, only you say that but if you provide the service then
I'll ride with you) - Designer interviews are among the very many services we offer, and
whenever we think a designer will return our emails, we try to score one.
Admittedly, I am now straining to come up with clever new questions (and
probably failing). Be that as it may, Christian was kind enough to entertain
my long-winded, circuitous questions, and hopefully his concise and to the
point answers will educate and interest you. Here we go:
MD: Ok, let’s get warmed up with some soft ball questions.
What can you tell us about your puzzling past? As in, how did you come
upon this strange hobby, how long have you been involved, and what made
you pursue it in such a very serious way?
CC: A friend had some basic puzzles that I was solving way
too fast in their opinion, then he gave me my first big puzzle that was
bronze Revomaze...I’ve been hooked ever since for the last 10 years and tried various
kinds of puzzle but I always go back to metal!
As soon as I started I wanted to create a puzzle that would be my
creation - the only criteria I had was to do something new.
MD: If you’ve read any previous PuzzleMad designer
interviews, then I’m sure this next question will be no surprise.
PuzzleMad bylaws mandate that I ask you, Chris, what are some of your
favorite puzzles and also puzzle designers? (I actually really enjoy
hearing the answers to this) (Ed - I didn't know we had bylaws but I'm interested in this too)
CC: William Strijbos, Jon Keegan, TwoBrassMonkeys...all
those and many others have very various designs that are unique to them.
MD: Keegan! You’re right. I have to get on that guy’s list.
Plant Cycle is a positively “mechanical” puzzle, in the truest and best
sense. Do you have an engineering or other technical background, by any
chance?
CC: No but I’m an electro-mechanic and I know my way around
big machinery.
MD: Designer creative process is always a mystery to me
(obviously). Assuming you do not formulate your puzzles sitting in the
lotus position atop a mountain peak, how DO you work? Does it involve
psychedelics, or just whole lot of graph paper? (Both answers are
acceptable)
CC: If I found an idea I write on paper, draw on paper,
think of the challenge to overcome to create it, then I get help from
family and friends to translate to computer and prototype.
MD: I need family and friends like that! So what stages do
you go through moving from initial concept to functional puzzle? Was
there ever a point at which Plant Cycle felt like it might not be
operational, or for that matter, feasible to produce?
CC: MANY times I had to change plans, for example I had to
redo the gears and gear plates of plant cycle to make it work . . . and
also had to change things in Father & Son and Billard a few times.
MD: Plant Cycle is constructed of 18 stacked
stainless-steel plates. The lamination technique is fairly uncommon. The
only recent puzzles I can think of that take this approach are (of
course) Rainier’s T10 and
Abhishek Ruikar’s Mimosa
(and Rex Perez’s coin releasers too, now that I think about it). Was
this the only practical way to make this puzzle? Did you consider other
approaches?
CC: I knew I could make it work and have something
different and didn’t want to go 3D-printed since metal is just my thing.
MD: Many metal puzzles involve a high degree of precision
between working parts. Metal lends itself to such precision in ways that
wood and plastics usually do not. Plant Cycle, however, does not seem to
require fine tolerances, by and large. I imagine this will be good for
puzzle durability and longevity. Was it intentional, or simply a natural
requirement of the mechanics?
CC: It’s intentional. Laser cutting stainless can only be
0.005-inch precise and when stacking layers the tolerances add up.
Plastic is just a fragile media and could be easily broken by
force...you can force mine all you want you won’t break it by
hands.
MD: It was very kind of you to include a reset tool, even
though as you note in the instructions, it is not at all necessary. What
made you decide to go ahead and include the reset shortcut? And did it
mean altering the design in order to include this feature?
CC: Although not necessary, there is a chance you could end
up in a bad sequence that would lock the puzzle if the tool wasn’t
there. I think it adds something interesting too for sharing and
resetting.

|
| Tiny hole. |
MD: It sure came in handy when I was taking pictures. One of the
other things I liked about Plant Cycle was that I was able to solve it. An
expensive puzzle presents a dilemma for the solver. You want it to be a
challenge worthy of the cost, but at the same time you don’t want it to sit
on the shelf laughing at you for years on end (Ed - oh Lord I have a few of those!). Plant Cycle hit it about right, in my estimation. How much thought did
you give difficulty level?
CC: I always try to put myself in the solver state of mind and
share it with friends and gather feedback. If I think it’s good, I go into
production...I’m not really a guy who worries too much in life.
MD: THAT is the correct answer, and Kevin and I should follow
your lead (But not until after this post)(Ed - if only I could!).
Plant Cycle presents a very slick and unfussy exterior; nary a screw or
fastener to be seen. If it is not a trade secret, how in the world do the
plates hold together?
CC: Each plate has 3 holes in each for alignment and 3 precise
pins go through all, then each end of each pin is welded - then the puzzle
is pressed by 25,000lbs to close gaps and the welds are ground to disappear.
(Ed - OMG!)

|
| Top plate. |
MD: Now I get the big machinery part! Grind the welds, of
course, why didn’t I think of that? Chris, I have to tell you, I love
those keys. The cut-outs are fantastic, and they really drive the theme of
the puzzle home in no uncertain terms. At what stage in development did
you settle on the grand “Plant Cycle” theme, and how soon after did the
cut-out idea follow?
CC: I create puzzle mechanics first then I think of a theme
that would work with it.
MD: Well, it’s hard to pull off great mechanics AND great
theme, but I think you nailed it. Spot-welding those 150 keys obviously
had to be done by hand. I don’t suppose you are a welder? If not, how hard
was it to find a machine shop that could do the kind of work you needed
done?
CC: My uncle Raymond has his own shop and it was him that
made it possible for me to do my creation and he still does a lot with me
for puzzle making.
MD: Regrettably, but quite predictably, I missed out on your
maiden puzzle - Father and Son Dueling Keys, the predecessor to Plant
Cycle. I understand from your website (or Facebook, can’t remember) that
Plant Cycle builds on that earlier puzzle. Can you share any lessons
learned from your first effort that you were able to apply to Plant Cycle?
CC: Solvers of my first design really had mixed feelings
about it. Some thought it was too easy, too loose, not finished to their
liking, but others found it exceptional. I work hard to listen to reviews
(bad reviews also give me lots to think about, so I like them too).
MD: I’m in the exceptional camp, no question; I wouldn’t
change a thing. But looking ahead, I know you are getting ready to produce
your third puzzle, Billiard. It looks like a move in a different
direction, and a very tantalizing one at that. What can you tell us about
Billiard?
CC: I’m not ready to produce, I finished producing 100 of
them. It’s a very precise and fine-tuned piece of work that I hope will
please my customers, both on precision/design/puzzle. It’s also harder
than the previous design
BILLARD:
Goal: Find the

Type: Sequential Discovery with 2 stages to complete, rising in difficulty
from step one to last. Use tools and logic to unlock and solve.
Made of: Hard anodized aluminum, all CNC.
Production Run: Limited to 100, all numbered from 1/100 to 100/100.

|
|
Billiard, needless to say.
|
MD: I think Kevin just swallowed his face mask (Ed - I inhaled it! Unfortunately this was out of my price range when it was released.). This looks and
sounds great, I can’t wait! Finally, Kevin and I (and possibly Felix Ure)
would like to order tungsten versions of Plant Cycle. Can do?Billiard? (Ed - Mike, you seem to have a fixation on Tungsten!)
CC: I’m not redoing old design, I want to move onto
different designs . . . each of my designs have particularities that are
hard to do so when I can move to another project I’m always happy...I also
know nothing about tungsten.
MD: That’s fine, because neither
do Kevin or I, just that its heavy. Any final thoughts?
CC: My
puzzles will stay limited: Father and Son Dueling Keys limited to 30 (sold
out); Plant Cycle will stay limited to 50 (sold out); Billard will stay
limited to 100 (sold out). People also have to understand that I’m only 38
years old, I got two kids and a full time job, and until I retire from my
day job in 15 years, I’ll keep making new puzzles if I get new ideas but
will keep the limit low...100 is my max and not sure I would make more
of a future design (Ed - I'm impressed that you can retire at 53!).
Thanks for all the interest you placed in my
creations.
Cheers,
Christian Cormier
Thanks Christian! That was great. I print these interviews out and store them with the puzzles, for a permanent record, so I really value your time and effort (and all past interviewees, you guys too!). Kevin, I, and the entire PuzzleMad readership appreciate it VERY much indeed. If I manage to solve Billiard, you may be hearing from the PuzzleMad Foreign Office, Hawaii Branch, once again. Prepare yourself! (Ed - erm, there is only the one foreign correspondent - I have singularly failed to find anyone who can/will write for the site).
Alright Kevin, time to wrap this beautiful Sunday up with your trademark words of wisdom and encouragement. Also, I forgive you for that Facebook thing from earlier 😊.
 |
| Water it every day |
Thank you so much Mike and Christian! That was an amazing article. I am very grateful for the work you put in to make something so interesting and somehow it's always a topic that I know almost nothing about. I have never managed to get hold of any of Christian's puzzles due to either timing or finance. I hope to play with one at an MPP next year if/when this bloody awful pandemic is over. Things had started to improve here in most of the country but has just recently taken a turn for the worst - I expect a new national lockdown to begin very soon in the New Year. No rest for me though as I still have to work and am now desperately looking back to choose my best puzzles of 2020 for next weekend. If you have any suggestions then please let me know.










 Type: Sequential Discovery with 2 stages to complete, rising in difficulty from step one to last. Use tools and logic to unlock and solve.Made of: Hard anodized aluminum, all CNC.Production Run: Limited to 100, all numbered from 1/100 to 100/100.
Type: Sequential Discovery with 2 stages to complete, rising in difficulty from step one to last. Use tools and logic to unlock and solve.Made of: Hard anodized aluminum, all CNC.Production Run: Limited to 100, all numbered from 1/100 to 100/100.