
|
|
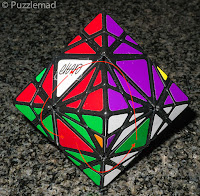
Eitan's Edge Turning Octahedron
|
I am working again (4th weekend in a row) and have produced this post in a bit of a hurry in advance. If there are any errors then please let me know.
Eitan Cher
has been responsible for a lot of fun in the PuzzleMad HQ and also a LOT of
angst! He has designed quite a few of my very favourite as well as the most
difficult of my puzzles. Despite all the angst, I absolutely adore what he
creates. The Edge Turning Octahedron (ETO) was purchased quite some time ago in
the expectation of fun and very quickly shelved when I discovered that it most
likely would cause angst! In general the edge turning twisty puzzles can be
mostly solved with a lot of intuition and only needing one or two fairly easy to
find algorithms for the very end of the solution. Overall, they have been some
of my most favourite of twisties for this reason:

|
| Edge turning cubes |
Why did I shelve it so quickly? One of the features of edge turners is the fact
that they jumble: that is, it is possible to perform partial turns to line up
intermediate cuts and then continue turning other edges which removes pieces
from their normal "orbits" and also can make pieces shapeshift wildly. This is
one of the reasons that I recommend them in my
"advice for a beginner" post. However, with the ETO it scared the pants off me:

|
|
Just one jumble!!
|
It was quite clear that this was going to be bloody difficult - probably too
tough for a relatively poor twisty puzzler like me. Eventually, I was
convinced by a number of puzzlers to give it a go and I decided to try a
non-jumbling scramble first. I really hoped that it would behave like other
edge turners and mostly solve by intuition. Off we go:

|
|
Oh Lord! What have I done?
|

|
|
Corners all sorted to ensure no parity
|
|

|
|
Attempting a single face
|
|
So far, with almost all the edge turning puzzles, I have tried and succeeded
in solving almost all of it by starting at one face and working my way up the
puzzle almost layer by layer until I have reached the top. Occasionally I have
had to intuitively build partial components and then move them up rather than
single piece at a time and then find out how to complete the endgame. Straight
away with the ETO, I struggled. It is almost impossible to build even a single
face by intuition without destroying previously positioned pieces. Above, was
about as far as I could get and I feared for the worst.
I thought this was going to go back on my shelf scrambled but I was fortunate
enough to have a massive explosion when I tried to make a turn without fully
aligning edges properly. I then had a good reason to completely dismantle it
and reassemble unscrambled and seek alternative methods. I really should have
done my "due diligence" first - but then I am well known for not being
terribly bright!
What most decent twisty puzzlers do when they have a new puzzle is explore it
before they scramble it and try and learn what different known sequences will
do. Since this was an edge turner, I felt confident that intuition would be
useful and did not bother with that crucial early exploration phase. Having
reassembled it, I could try again and do it properly.
The first thing I often do is sequences of turns around a face or corner and
see what happens after 2,3,4,...x turns and if nothing seems to be useful then
I can very easily backtrack.
I very quickly found this lovely sequence which certainly looked like it might
be useful - turning the blue/white edge and the purple/white edge sequentially
three times cause 2 adjacent centre flat triangle swaps with the adjacent edge
wings. This might be useful.
As you can see - the end result of the simple 8 move CPS is to 3 cycle the
centres (plus muck up some edge wings, but with no effect on the corners and
centre flat triangles. This tells me that if I can find a way to solve the
corners and flat triangles first and edge wings last then I have an approach
to the solution.

|
|
3 cycle these composite corners takes 4 moves
|
|

|
| Do the same F to B then undo |
|
Next thing I did was look for any easy
commutators. This was not terribly difficult - it is easy to perform a 4 move sequence of R, L, R, L to swap composite corners as done above left. If I can isolate one of those edge wings in the top and then undo it all then I have a commutator. Luckily isolating that edge wing is very similar (I just perform a F, B, F sequence and then I can undo the original sequence. The end result is to create a 3 cycle of edge wings. I'm getting closer. I can place and orient corners by intuition, I can place the centres and the edge wings. I now only have to find a way to move the flat centre triangles (either alone or with other pieces) and then I have my whole approach sorted. This takes me quite a while.

After a lot of fiddling around and desperately trying not to forget what I moves I have made so that I can always undo them, I discover a very similar sequence to the edge wing commutator. If I turn the front edge and then follow this with a R, L, R and then undo it all, I have another commutator. This time it is not pure - as you can see to the left, I have moved centres and flat centre triangles with an adjacent edge wing in a 3-cycle.
This gives me my whole puzzle solution:
- Solve the corners
- Solve the flat centre triangles (the sequence moves everything apart from corners)
- Solve the centres (the sequence doesn't upset corners or flat triangles)
- Solve the edge wings (the sequence doesn't upset anything else)
Is it quite as easy as that? Erm... not really! Placing the corners is very simple except that there are lots of positions that places them in positions that the flat triangles cannot reach - they are in orbits as one would expect of an edge turning puzzle. It is ESSENTIAL to get those corners right first and seems to take me quite a while to get it right. I found a parity where 2 pairs of centre flat triangles need to be flipped. This cannot be done with the 3-cycles but luckily I had found my simple technique as the first thing I had found. All that was needed was to 3 cycle the pairs so that the were either side of a single centre. The centre positioning is pretty simple and then the edge wings are just plain arduous - as you work your way through, you need more and more complex setup moves to ensure the pieces I wanted to move are in the correct positions. Eventually the setup moves are so complex that I have to write them down before I perform the algorithm otherwise I will forget what I have done and then be unable to undo it.
In the end - I have my solved Edge turning octahedron and a huge sense of relief! I have to say that yet again Eitan has created a most fabulous puzzle and any serious twisty puzzler should buy a copy. It is not an easy puzzle (certainly no intuitive like most edge turners) but definitely solvable with a bit of experimentation. I really need to add another chapter to my advice to a beginner series to include a few of the puzzles produced since my original post. I may need some help with that if anyone wants to help me. Now I need to get the courage to try a jumbled scramble and solve. I suspect it will take me some time to get the courage together for that!!!










My solution to this ist sligtly different. I solved the corners first, then the central triangles, by swapping two pairs, plus setup moves. Next, I solved the flat triangles, by swapping two pairs, as shown above. Finally, für the wings, I used a different 3way permutation, based on the flat triangle pair swap, plus one edge turn. The last stage required rather complicated setup moves, finding more algorithms for this will simplify things a Lot.
ReplyDeleteWow! That’s an interesting approach. I’d be interested to see that if you have seen it anywhere on YouTube. Let me know.
DeleteKevin, did you receive my emails?
DeleteYes, very clever. I’ve not had much time to reply to my puzzlemad emails. I’ll get back to you soon.
Deletehi could you elaborate more on fixing thr last two pairs of wide wing parity
ReplyDeleteUnfortunately, after 2 years I have no recollection of how I solved this puzzle. I probably should try again if I find some time. There are a couple of very good YouTube tutorials that may help you.
Delete